C++
, ,
Source
Edit
History

C++11中的负数取模问题

Catalogue

给你一个整数 n ，以二进制字符串的形式返回该整数的 负二进制（base -2）表示。

注意，除非字符串就是 "0"，否则返回的字符串中不能含有前导零。

示例 1：

1
2
3
输入：n = 2
输出："110"
解释：(-2)^2 + (-2)^1 = 2

示例 2：

1
2
3
输入：n = 3
输出："111"
解释：(-2)^2 + (-2)^1 + (-2)^0 = 3

示例 3：

1
2
3
输入：n = 4
输出："100"
解释：(-2)^2 = 4
  • 一种最简单的解法如下：

与转化为二进制没什么区别，都是除基取余，倒序排列。
不过负二进制的余数可能有0，1，-1，而表示上不能有负数，所以在余数为-1时，要转化为1，同时商+1即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    string baseNeg2(int n) {
        string ans;
        while(n)
        {
            int remain=n%(-2);
            ans+='0'+abs(remain);
            n=remain<0?n/(-2)+1:n/(-2);
        }
        reverse(ans.begin(),ans.end());
        return ans.empty()?"0":ans;
    }
};
  • 这里涉及到n%(-2)和n/(-2)的运算结果。C++ Primer第五版中是这么说的：

image-20230406133817963

  • C++ Primer中的这两段话可以归纳为如下两点：

    1. 在C++11中，除法运算m/n的商一律向零取整。此时，m/n、m/(-n)、(-m)/n、(-m)/(-n)这四个表达式的运算结果的绝对值均相等，运算结果的符号取决与被除数与除数是否同号，同号得正，异号得负。例如：21/5=4，21/(-5)=-4，-21/5=-4，-21/(-5)=4。换言之，商的绝对值乘以除数的绝对值一定不超过但最接近被除数的绝对值。

    2. 根据1可以推出，取模运算m%n的结果永远与m同号

  • 回到LeetCode 1017这道题。当我们使用”除-2取余法“时，可能得到的余数为0、1、-1。由于最终结果为“-2的非负整数次幂相加”的形式，当余数为0或1时，可以直接作为结果中的一位；当余数为-1时，必须将其转换为非负数，方法为：让被除数多除一个-2，商加1，由于多除了一个-2，余数就需要减去一个-2，即余数-1加上2变为1。

  • 本质上，解决这道题需要使用“正数除以负数，商向0取整；负数除以负数，商向无穷取整”的除法规则进行除-2取余，这样得到的所有余数都是正的，能够组合成“-2的非负整数次幂相加”的形式。然而由于C++11标准的除法一律向0取整，我们需要在每次得到负余数的时候多进行一次调整，以符合题目要求的除法规则。

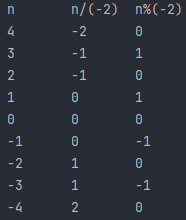
  • 为加深理解，再附上C++17中不同整数除以-2的运行结果：

image-20230406140637592