bzip2相关论文阅读笔记

Parallel Data Compression With Bzip2（分块压缩）

压缩算法的分类

• 字典算法
  • LZ77（ZIP、GZIP）
  • LZW（自适应）
  • 并行研究
• 基于统计的算法
  • 建模阶段->编码阶段
  • 基本建模技术
    • 符号频率
    • 符号上下文
    • 符号排名
  • 算术编码器：PPM部分匹配预测
    • 当前（2004）文本数据的最佳无损压缩算法
    • 有限上下文统计建模技术
    • 使用输入流的前一个字节来预测下一个字节

Burrows-Wheeler Transform

概念

• 块排序、无损数据压缩算法，对输入块执行可逆变换
• 不执行任何压缩，但以某种方式修改数据，使其易于使用二级算法进行压缩
• 变换后的块包含与原始块相同的字符，但是形式易于压缩，例如相同字符分组在一起

原理（逆过程见Parallel algorithms for Burrows–Wheeler compression and decompression）

• 过程

  1. 源字符串S，包含N个字符

  2. 将S旋转（循环移位）N次，将旋转过程中生成的N个中间串进行字典排序

  3. 提取这N个串的最后一个字符，组合成串L

  4. I为源串S在排序后的串列表当中的索引

• 选择分块大小，至少2KB。增大块大小可以增强有效性

• 视为三个阶段

  1. 排序阶段
  2. “Move-To-Front”阶段
  3. 压缩阶段

性能

• 内存消耗：9B内存/1B数据+700KB常量
• Move-To-Front编码器的选取影响压缩率：不同的排序顺序和源字母表的顺序
• 最佳性能：O(logn/n)，优于LZ77、LZ78

应用

• BZIP2：BTW+哈夫曼编码
  • 压缩率优于基于字典算法的LZ77/LZ78
  • 在基于统计算法的PPM中，压缩率接近，但快很多

并行BWT

• 并行排序
• 分块BWT
• 结合上述两种方法
  • 性能取决于处理器数量，需要进行测试

并行BZIP2（PBZIP2）

• pthread
• 分块
  • 块在内存中以生产者/消费者模型、FIFO管理
  • 每个处理器读取块，执行BWT，然后释放内存

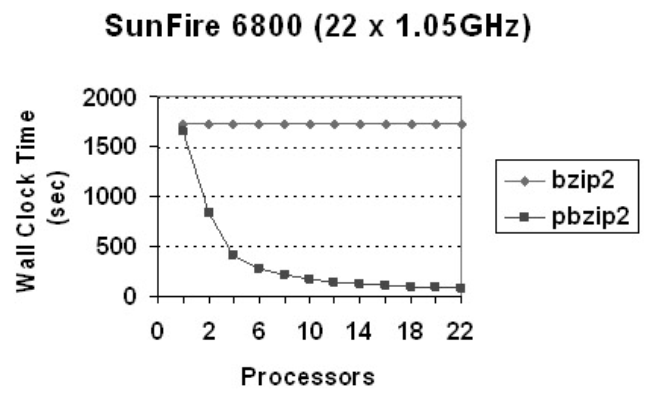
实验

• 随着处理器数量的上升，pbzip2压缩时间减小。减小到大概12个处理器就增长缓慢了。

Practical Speculative Parallelization of Variable-Length Decompression Algorithms（分块解压）

解决的问题

• 如果压缩时采取块级并行，那么解压的时候，在完成对一个块的解压之前，无法确定这个块的边界

• 相关工作的解决办法：

  • 在压缩块的末尾插入填充位，或者加入提示：只适用于修改后的压缩器
  • Klein和Wiseman利用Huffman编码的自同步特性：只适用于静态Huffman编码
  • 块边界位置在一个输入之内或跨不同输入的相关性几乎为0，因此难以应用domain-unaware value prediction algorithms

• 提出SDM：一个有效预测区块边界的新算法，和能够实现高效区块级并行解压的运行时系统

  • 思考：运行时系统能否被很好应用于移动端？可以，因为华为手表的升级程序是官方定制的。本文的实验是在嵌入式平台上做的
  • 不需要修改压缩器

动机

变长解压算法

• 即使压缩时定长分块，生成的每个块大小也不一样

• 解压时存在的依赖：

  

基于值预测的推测并行化

• 三种方法均无效：

  • pos变量在一段时间内或者不同的输入之间构成几乎0的相关性，使得值预测无效

  • 在一个块末尾计算pos的复杂性与解压整个块的复杂性相当，使得提取预测器函数开销太大

  • 复杂的依赖模式和有限的程序分析能力使得automatic distiller也无效

• 目标：三个部件

  • 自定义值预测器：以高置信度和低开销确定每个压缩块的起点
  • 运行时错误预测检测和恢复机制
  • 易于使用的并行化API：将现有的变长解压算法转化为基于值预测的推测并行代码

块边界预测算法

第一种：基于部分解压

• 不适用于bzip2，略

第二种：基于模式匹配

• bzip2包含一个48比特的魔数头，用于标识一个新的被压缩块的开始；并且不存在块间依赖。采用模式匹配

SDM执行模型

SDM三阶段流水线

• 三种进程：扫描器、解压器、合并器
  • 主进程创建并配置每个阶段
  • 主进程本身作为合并器
  • 默认：解压进程数量==可用核心数量
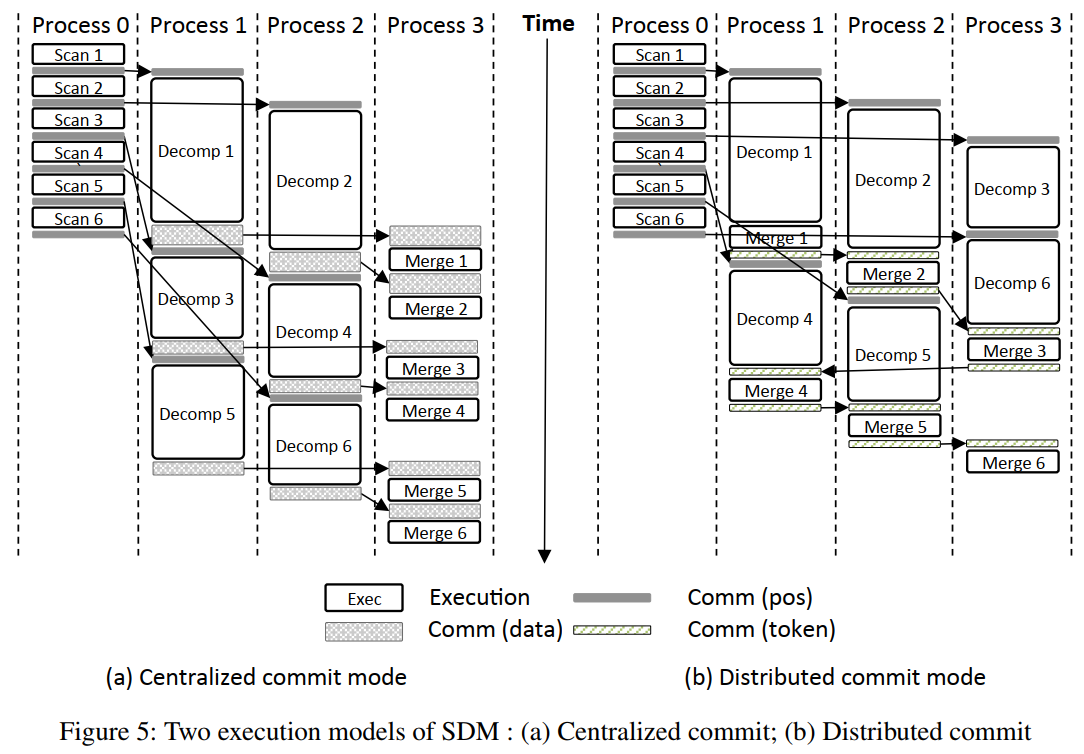
• 在拥有大量可用核心的多核嵌入式平台当中，使用集中式提交模型（一个合并器）
  • 解压-合并通信可能成为性能瓶颈
• 由于上下文切换和内存空间开销，核心数较少的平台无法从额外的进程受益，需要使用分布式提交模型
  • 将解压器和合并器融合
  • 如何顺序提交：定义一个提交令牌在进程间传递。一个块解压后在本地缓存，等待收到解压令牌后才进行提交

错误预测检测和恢复

• 由合并器负责：将从扫描器收到的预测值与解压器收到的实际值进行对比

• 如果检测到一个错误预测，所有的扫描器和解压器都被停止，程序的其余部分顺序执行

SDM API

• 略

实验

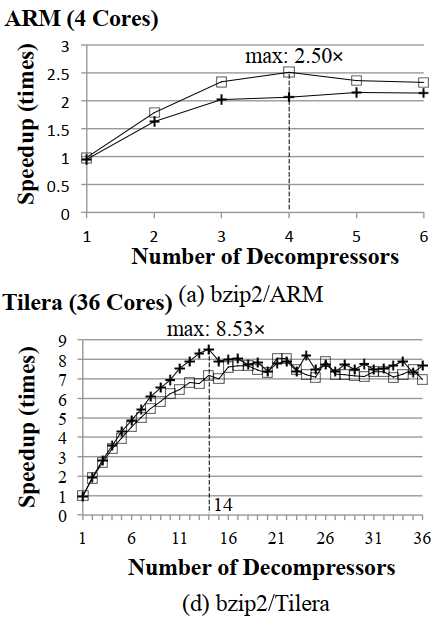
• 错误恢复的性能：对于bzip2，如果误判发生在输入文件的开头附近会造成轻微的性能下降；但是在大多数情况下都比顺序执行要快

Parallel algorithms for Burrows–Wheeler compression and decompression（块内压缩和解压）

贡献

• 第一个应用于BW压缩和解压缩问题的PRAM算法
• 相比Parallel Data Compression With Bzip2，解决了整个输入的BWT问题，而不是分块
  • 本方法与分块方法正交，因此还可以在单个块上叠加应用本方法

预备知识

BST

正过程

• 见Parallel Data Compression With Bzip2

逆过程（IBST）

• 定义S^BST为BST正过程生成的串，M为BST正过程排序后的矩阵（显然M为方阵）。显然S^BST为M的最后一列

• 需要一个符号表示字符串末尾，且这个符号的字典序最小。对于英文字符串，可以取ASCII序在英文字母之前的”$“。在Parallel Data Compression With Bzip2这篇论文当中则是用一个数组记录

• 迭代法生成M的每一列，迭代N次后，取M的第一行即为原来的S

  1. 为了生成M的第一列，将*S^BST*进行稳定排序。

  2. 为了生成M的前两列，执行下列两个步骤：

     1. 将*S^BST*插入到第一列的左边

     2. 对M的前两列进行下列定义的排序：

        • 如果两行的第一个字符不同，则根据第一个字符排序
        • 如果两行的第一个字符相同，不动

  3. 重复2直到生成M

• O(N)复杂度方法

  • 图示思路：将M中的所有*$写出来；然后旋转每一行，使得$位于最后一列；此时，从左往右读就是源串S*
  • 伪代码：有点难读懂，先略过

MTF

正过程

• 给定一个字符，MTF将每个字符替换为：该字符本次出现与上次出现之间，不同字符的个数。为了保证该定义有效，规定字母表在*S^BST*之前以某种顺序出现。

• 定义*L_i为S^BST*的前i个字符中，每一个不同字符以其最后一次出现的位置倒序生成的列表，且考虑上述假定的前缀。

• 伪代码：

  1. L := L₀（即假定前缀的倒序）

  2. for i := 0 to n - 1 do

     1. j := S^BST[i]在L中的索引

     2. S^MTF[i] := j

     3. 将L[j]移动到L首部

• 目的：由于BST保证了同个字符的出现位置相近，MTF生成的是小整数序列，即小整数出现频率很高。因此该序列适合于进行Huffman编码。

逆过程

• 伪代码：
  1. L := L₀
  2. for i := 0 to n - 1 do
     1. j := S^MTF[i]
     2. S^BST := L[j]
     3. 将L[j]移动到L首部

Huffman编码

正过程

• 伪代码：
  1. 把字母表中的每个字符在S^MTF中出现的次数进行统计，生成频率表F
  2. 使用频率表F构造码表T。对于任意两个字符a、b，如果F(a) < F(b)，则|T(a)|>=|T(b)|
  3. 将S^MTF中的每个字符用T中对应的码字代替，生成S^BW。S^BW即为整个压缩算法的输出
• 思考：
  • 源串中一个字符需要一个字节来存储；Huffman编码后字符由几个0、1比特表示，只需要几个位来存储。如果Huffman的平均字长小于8，则源文件体积能够减小。

逆过程

• 显而易见。参考解压的并行一章

压缩的并行

BST

1. 构建后缀树

   • 性能：

     • Sahinalp and Vishkin的算法：O(log²n)时间，O(n)工作，O(n²)空间

     • 可以将空间复杂度降到O(n^1+ε)，当时间增加1/ε倍

     • Hariharan的算法：O(log⁴n)时间，O(n)工作，O(n)空间

2. DFS遍历后缀树，生成后缀数组SA

   • 欧拉旅行技术
   • 相同复杂度界限

3. 按照如下公式生成*S_BST*：S^BST[i]=S[(SA[i]-1)_{mod n}], 0<=i<n

   • 性能：O(1)时间，O(n)工作

MTF编码

• 定义

  • MTF(X)：同L_i，只不过L_i针对的是输入串的前缀，MTF(X)进行了扩展，针对任意子串X
  • x⊕y： 把在y中出现过的字符从x中移除生成一个列表，然后把这个列表拼接到y的后面
    • 注解：y不动，x中单独出现的部分拼在y后面

• 观察

  • MTF(c)=(c)
  • MTF(XY)=MTF(X)⊕MTF(y)

• 目标：计算所有L_i，即计算S_BST（考虑假定前缀）所有前缀的MTF

• 步骤：

  1. 将*S^BST*的每个元素看成初始的列表，从下往上，在一棵平衡二叉树中用⊕运算符两两合并列表，直到根节点

     

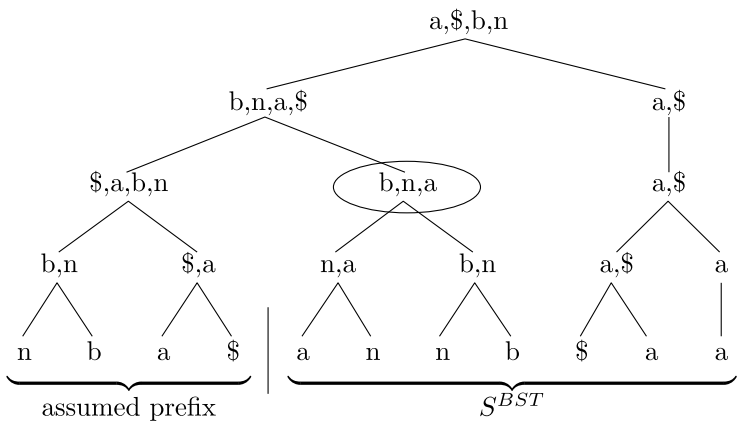
  2. 从上到下，计算每个节点的⊕运算前缀和（从根的最左叶子节点到当前子树的最右叶子节点）。叶子节点的前缀和即为L_i

• 性能：

  • 时间复杂度：O(|Σ|logn)时间，O(|Σ|n)工作
  • 空间复杂度：n|Σ|
  • 权衡空间和时间的方法（划分粒度）：选取一个k<n，只排序*L₀、L_k、L_2k*、……。此时空间降低k倍，时间相应增加k倍

Huffman编码

看了，但暂时不关心，没记录

解压的并行

Huffman解码

• 难点：由于Huffman码字是变长的，需要选定*S^BW*的分割位置
• 定义l为最长码字的长度。不失一般性，假定|S^BW|能够被l整除，我们要把S^BW分割为若干个长度为l的切分。目标是选定每个切分的开始位置
• 计算开始位置需要两个步骤：初始化->前缀和计算
  • 初始化阶段
    • 从S^BW中的每个位S^BW_i开始执行解码（解码一个码字）。对于每个i，获得一个停止解码的位置j。记为i->j
  • 前缀和计算阶段
    • 对于形如a->b、b->c的映射，将他们合并为a->c
    • 合并后，0指向的所有位置都是开始位置，保存到集合V中
• 实际解码阶段如下：
  1. 部署n/l个处理器，每个处理器指定集合V中一个不同的开始位置，并行执行哈夫曼解码，直到到达下一个开始位置。解码后先不写到内存。O(l)时间，O(n)工作
  2. 使用前缀和为每个处理器在S^MTF的输出分配空间。**O(log n)时间，O(n)工作
  3. 重复步骤1，将输出写到*S^MTF*。O(l)时间，O(n)工作
• 实际解码阶段：O(logn+l)时间，O(n)工作
• 思考：这么细的划分粒度值得吗？partition的块数太多了，是否可以不要分那么多

MTF解码

• 与编码类型
• 性能相同：O(|Σ|logn)时间，O(|Σ|n)工作

IBST

• 涉及Cole and Vishkin的整数排序算法

  • 性能：O(|Σ|logn)时间，O(|Σ|n)工作

• 性能：O(|Σ|logn)时间，O(|Σ|n)工作

实验

• 这篇文章没有做实验
• 实验在另一篇文章Empirical Speedup Study of Truly Parallel Data Compression

Empirical Speedup Study of Truly Parallel Data Compression（块内压缩和解压）

实验

• 在XML计算平台的64-TCU FPGA上运行时，解压性能总体上看甚至略微下降了；在模拟的1024-TCU上运行时有提升

  

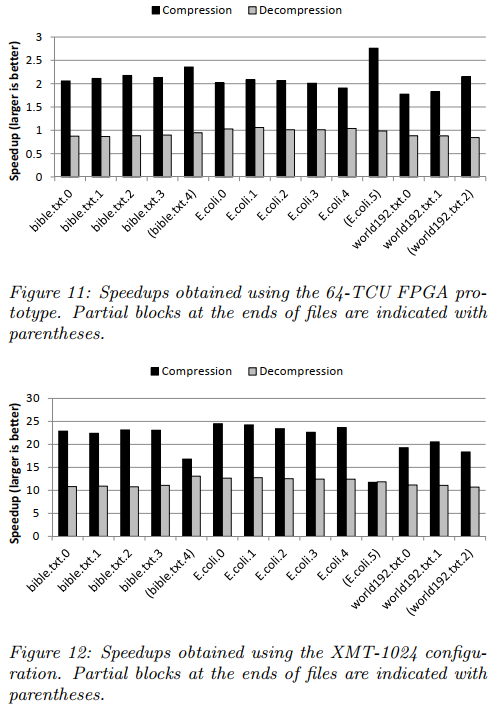
• 思考：这个是在专用的并行计算平台上运行的结果，对移动端的参考价值？

Parallelizing Bzip2: A Case Study in Multicore Software Engineering（学生作品）

简介

• 一个多核软件工程课程的最后三周，8名计算机科学专业的研究生2人一组进行比赛，对bzip2算法进行并行化
• 针对压缩

Team 1

• 发现细粒度的并行化不合适，需要大量努力重构代码
• 尝试用类重构，但最后ddl到了还是换回没有类的版本，整合了Bzip2SMP的一些并行化思想

Team 2（winner）

• 重构花了很长时间，最后一天才写并行
• 生产者-消费者模式+pthreads
• 流水线没时间写了

Team 3

• master-worker方法
  • master程序向一个缓冲区填充块，worker程序从缓冲区中取出块来进行压缩
  • 线程同步和文件顺序输出遇到困难
• 超时了

Team 4

• 用openmp，性能较差
• 大部分时间花在理解代码

Lessons Learned

• 并行化之前需要重构代码

• 增量并行化没有作用

  • 例如用OpenMP在代码开头加pragma

• 研究关键路径行不通

  • 例如用profile工具
  • 顺序实现通常涉及设计选择，排除了并行化可能需要的自由度
  • 因此，仅仅研究顺序实现是不够的，还需要研究规范

• 细粒度并行不是唯一选择

  • 例如，关键路径上循环的并行化只产生很小的速度提升

• 寻找高层次并行化

  • 例如，引入生产者-消费者模式或者master-worker模式
  • 代码实现涉及的细节更多

• 试错是有风险的

• 并行化不是黑色艺术

Advice

• 并行时考虑多个层次

  • 不然就会“一分钱一分货”

• 如果从0开始写顺序代码，要为并行化考虑

• 多练习

相关前置知识

• 自适应（动态）哈夫曼编码与解码过程_菜鸟的逆袭之路的博客-CSDN博客_动态哈夫曼编码
  • Parallel algorithms for Burrows–Wheeler compression and decompression中使用的Huffman编码是动态的，因为没有提到要存Huffman树
• 并行算法科普向 系列之二：前缀和，fork-join 和矩阵乘法 - 知乎 (zhihu.com)
• 值预测算法：见文章Value Prediction for Speculative Multithreaded Architectures
  • Practical Speculative Parallelization of Variable-Length Decompression Algorithms中提到值预测算法不可用
  • 值预测技术基于以下推测：在大量的时间内，值倾向于重复，或者遵循一个已知的模式。因此，如果使用恰当的机制，值可能能够被正确地预测。这些机制的基础是存储反映近期观察到的历史信息的表格
  • 分类
    • 基于指令的值预测器
    • 基于追踪的值预测器

相关实现

bwtzip

• bwtzip - nuwen.net
• 他是高度模块化的，或许可以帮助我后续的代码重构和实现

相关会议

• Data Compression Conference：IEEE Xplore - Conference Table of Contents